How are the Fourier Series, Fourier Transform, DTFT, DFT, FFT, LT and ZT Related?

So how are Fourier

series

, Fourier

transform

, discrete-time Fourier

transform

, discrete Fourier transform, fast Fourier transform, Laplace transform, and z transform

related

to each other? So let's start with the Fourier

series

that we're going to start in continuous time. So this is where we have a t for continuous time and the Fourier series applies to signals that are periodic, so I'm going to draw here a signal that is periodic, meaning it repeats with a period and the period is important and it is of fundamental importance. zero omega frequency, so I'm going to write the equation here. I won't write the equation for all the transformations, but I will for this one just to make a point here, so this is from k equals negative infinity to infinity of a k times. e al j k omega naught t and here omega naught is the fundamental frequency, so what is the Fourier series?

Well, again, I'm not going to give all the details. There are many videos on the channel which you can find in the notes below this one. video, but for this case of continuous time Fourier series with a periodic signal, then the Fourier series is written in terms of k, so this axis here is k, so it is not a frequency axis, this is an index of these a, so we are plotting a k as a function of k so it is an index of the case and the index is

related

to multiples of the fundamental frequency, okay, and in this case it is discrete because they are discrete, it is a discrete sum of multiples of the components of the fundamental frequency, okay, so it's discrete and it's a periodic, so this is not a periodic function uh of k, it's a periodic function, okay, so this is one of the properties of the Fourier series, so when does it apply again?

The important thing is that it applies to periodic signals and where the period here is capital t. 2 pi divided by that fundamental frequency omega nothing good so that's the Fourier series in continuous time what about the Fourier transform? Well, the Fourier transform is a generalization of the Fourier series for signals that are not periodic and the most common signal that we or a One of the most common that we consider here is a square function, it is very important for digital communications in the ones you turn something on and off and all kinds of other electronic devices and other situations, so in this case, what is the Fourier transform?

Well, it is not periodic and that is when the Fourier transform comes into play, it is more general than the Fourier series and in this case you are probably familiar with the sink function. I'm going to plot the magnitude here and it's important to remember that there is also a phase component, but in this case, some differences with the Fourier series is that this is not this, this is the actual frequency represented in radians when plotted with omega so this is the actual frequency and they are all different frequency components that are possible whereas for Fourier series it was just the multiples of the fundamental frequency so that is an important difference between Fourier series and the Fourier transform, so all frequencies are possible and they can all contribute to these periodic or non-periodic signals, so this is what we call the continuous-time Fourier transform, so the ct ft and this one up here was continuous time Fourier series often ctfs, okay, so this is also important to note that here I will put a magnitude with a point there that there is also a phase component, but we often only plot the magnitude of the Fourier transform, so it's an important thing to remember and of course also this is continuous, as I said, with all possible frequencies and it is periodic, the signal is aperiodic in time and it is also periodic in frequency, OK?

One thing, although we can define the Fourier transform for periodic signals, one common thing we do is that it is one of the fundamental basis functions. I'm going to draw it here, so this is the Fourier transform for the periodic signal. Generally, one thing I should say for the Fourier transform is that it is defined for signals that have finite energy. Now these periodic signals do not have finite energy, but we can define them using the delta function. We can define them in a particular way under the Fourier transform, so there is a definition for periodic signals under the Fourier transform and in this case for this cos wave you may be familiar with it and this is where I mentioned with the delta function that in the Fourier transform the magnitude of the Fourier transform in the frequency domain is now actually it's continuous and it's impulsive, so when you have a periodic signal, if you're doing the Fourier transform, you get an impulsive Fourier transform , we call it impulsive, where we have these delta functions and this is omega zero and minus omega zero and again for To learn more about what exactly it is, check out the videos in the link below.

Well, this is for continuous tense. What about discrete time? Well, in discrete time we have things that we use little of. We normally use the small n to index the discrete time y. We're going to start with the discrete-time Fourier series, so again the Fourier series deals with periodic signals, so here is a signal that is periodic. This signal here is periodic. I'll try to draw one here that is periodic. Okay, so this is a discrete time, so it only exists for integer values ​​of n in the time domain, that's why it's called discrete time and it's periodic, so we're looking at the Fourier series, this is the series of Discrete time Fourier dtfs in this case is a discrete similar to continuous time this time it is discrete but it is periodic so it turns out that this is periodic so why is it periodic? uh let me draw something here that's periodic um it's just a sketch representation uh it's not exactly I'm not exactly trying to replicate the trans

fourier

fourier

series for this function here but I'm just trying to indicate that it's periodic , so this is a periodic function here and the period of this function is n, so this is capital n is the period of that function uh where you have the Fourier uh the period here relates to uh the fundamental frequency sorry relates to 2 pi divided by capital n okay so this was the period here also as n so this is the period n and this is in the frequency domain it also has a period n actually, I haven't outlined enough points here to be exactly precise, but I think you'll get the message, so this is in the time domain, the discrete.

Time domain and Fourier series are discrete and periodic with period n so this is a point to note, as I mentioned the basic functions repeat when you have discrete time signals and to learn more about why are they repeated, there are many links. in the description below where you can find information about that, okay, now let's look at the equivalent of this here, now we have the discrete time Fourier transform, so what do we look at here and a common one equivalent to this here. I'm just drawing it with an offset here because I have to squeeze one more on the discrete side, so I hope you recognize that this one will be equivalent and will match this one. over here um in terms of this is the discrete time Fourier transform, uh, sorry, so this is the transformation line and this is the discrete time transformation line, so here we have, it's important not to forget these zeros here.

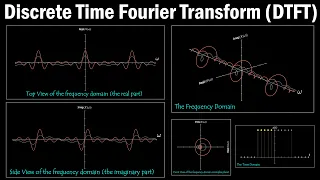
So in this case, this function is periodic, therefore we need the Fourier transform as we had it in continuous time and it is zero for all times other than these. Here I'm just using this square function as an example in this. case again, the basic functions are repeated, what does this mean? Well, I'll draw it out in a minute, but first I'll make it clear that the Fourier transform of a discrete time signal that is periodic is a continuous function, etc. Here it is, it is continuous and exactly the same reason why here this was discrete in terms of the Fourier series and then the Fourier transform was continuous and had the possibility of containing all the different basis functions at all the different frequencies and this is exactly the same in the case of discrete time and again if that is something you would like to know more about there is a video in the link below in the description below and this is because the basic functions they repeat, this is periodic and the period is 2 pi, so this is minus 2 pi and this is 2 pi and this is a zero here and again we are plotting the magnitude so this is the Fourier series has discrete is discrete in the Fourier series uh the Fourier transform even though it is discrete time the Fourier transform is continuous, okay, so we have periodic signals.

Now, what about the discrete-time periodic signal to match this one here? So we said that the Fourier transform was for periodic signals. Signals that are not periodic, but you can define them as. the same thing in continuous time, you can define the Fourier transform in discrete time for a periodic signal, so let's choose one here as an example, let's choose one that matches this one here, so let's divide cos omega naught n, so this function here because omega naught n looks like this function here where it goes follows a cos shape, so I'm just drawing that curve, there's an indicator of where the points are, I'm not trying to fill it in, just these are the actual discrete points here of a cos function in discrete time, okay, so this is just trying to sketch that out there, so this is in discrete time, a periodic function can have a Fourier transform, so let's remember that it is in this case because it is a function periodically as in this case. here the Fourier transform will be impulsive, so here in discrete time the Fourier transform of a discrete time signal is still continuous, so it has the potential to have all values ​​of omega, but because it is periodic, it will be impulsive and So here, for example, we're going to have matches with the continuous-time version, we're going to have these two impulse functions at omega zero and minus omega zero, but again, because the basic functions repeat, we're also going to have those that repeat our round centered at 2 pi and also repeated centered around minus 2 pi, so this is minus 2 pi, this is 2 pi and this is the Fourier transform of a discrete time periodic signal, so what matches.

You can see the similarities here in continuous time. the continuous time cos waveform has a Fourier transform that only has two impulses in minus omega norton omega nothing in discrete time also has two impulses, but since it is in discrete time the basic functions repeat in 2 pi and are multiples of 4 pi 6 pi 8 pi and so on, as well as minus 2 pi minus 4 pi and so on, this is the equivalence between continuous time and discrete time. Well, now we have covered Fourier series and Fourier transform and discrete-time Fourier transform, so what is this? something else called discrete Fourier transform.

Well, the discrete Fourier transform is primarily what is implemented on a computer and this is because a discrete Fourier transform is just an equivalent of the discrete-time Fourier transform, but it only has a finite number of samples, so which in this case here because this is what you've stored and what you've measured and what you've stored on a computer, of course, you don't actually have an infinite number of samples, so you really only have a finite number and so If you have sampled, what does the discrete Fourier transform do? So this is the dft, what is the difference between this and the discrete time Fourier transform?

Well as I say you only know the samples between two limits so you don't know anything about the samples here it's not that they are zero like they were here they just don't exist all you've done is sample over a finite period of time , so you have a finite number of samples, so there is no arrow here it's not at index n going to infinity or something like that it's just above the finite sampling period of capital n and what does dft do well ? What has been sampled is assumed to be periodic, so these samples are assumed to repeat as if they were like in the previous example, as if they were a complete periodic waveform going from minus infinity to infinity, all of which You've done is sampled a finite number of samples, which is all you can do in practice, but dft implicitly assumes that you've sampled an entire period of something that is periodic and continues for an infinite amount of time, so how much more Fourier, the discrete Fourier transform will give you exactly the same result as the discrete Fourier transform, assuming that for the periodic signal, if this The signal here were if this were because you have tried, then the dft process assumes that it lasts for always, soyou will get and can do this in Matlab or other Python programming languages ​​etc.

You'll see that you returned an exact version of the discrete-time Fourier transform when you do the discrete Fourier transform. Now you can see what happens. This is the case if you have sampled for an exact period if you had taken fewer samples than a full period. period then you wouldn't have a waveform that would be exactly equal to cos because you would have a shorter waveform that would then not repeat periodically to form a cause because it would have discontinuities at the ends and then you wouldn't get an exact match in the domain of the frequency and again there is a video about it on the channel about the dft.

Well, what's the fft? Well, the fft is exactly the same as the dft. It's just a smart way to improvise by implementing the dft in a quick way. with the use of less calculations than the full dft formula, so the fft or fast Fourier transform is the same as the discrete Fourier transform, it's just a more efficient implementation for you to get the same relationship there, well, in the last two transforms of the Laplace transform and the z transform and in the Laplace transform, how is that related? The Laplace transform is continuous time, the z transform is discrete time, so let's look at those two now, we said before that the Fourier transform applies to signals that have finite energy, so what do you do if you have a signal like this one that continues to oscillate and increase, so this is like, for example, an example is positive? feedback in a microphone system where the signal continues to increase in its amplitude as time passes.

This signal, if it continues like this forever, will not have finite energy, so in this case, instead of doing the Fourier transform, in this case we generalize and we, instead of having j omega in the formulas, which I have not shown the formulas here, but you can look them up instead of having j omega in the formula, we replace that with another variable s which is simply equal to sigma plus j omega, so it's almost the same as the Fourier transform, only there is an additional component, an actual component that you are replacing it in, and again there is a video on this that explains the region of convergence, so mainly here we draw the region of convergence instead of drawing the transform because now we have an additional variable , so not only do we have amplitude and phase, but we also have a real and imaginary component of the transformation variable, so we normally say this is real and imaginary and you are you.

You've probably seen things where there's a vertical, there's poles and zeros and a vertical line from the poles and you may have seen a cross area which is the region of convergence, what that means is the error, the region of s values ​​that I can see that the sigma values ​​are greater than this number here, for example, I would give the entire area to the right, so these are the sigma values ​​for which the transformation converges, for which you can evaluate the integral and it turns out which if it includes if this region of convergence includes the vertical axis when sigma is equal to zero then you actually have the Fourier transform so you can see here if sigma is equal to zero then you would have exactly the same thing as the Fourier transform and that would be look along this line here, so if we take that line, this is where this becomes greater here and this stays, if we take this line and rotate it before sigma equals zero, then we would have the transform of Fourier, so I think about the Fourier transform that we have.

I've drawn this line here, if I rotate it up so it's vertical and then move it like this, then it will live on top of that line there and the other values ​​for other sigma values ​​will have other shapes and there will be a smooth line. function and again to learn more about this, there is a video on the channel, so the final is the Laplace transform, so the final is the z transform. Okay, the z transform is equivalent to the Laplace transform, but only for discrete time. signals, so if we had a signal that increased as time went by or as samples went, it's not a finite signal, it's a signal that lasts forever, like this discrete time signal up here, so if this signal here it doesn't have finite energy, again like with Laplace, but in discrete time we can replace and again you can see more details about this, but we can replace the e to the j omega with an r multiplied by e to the j omega, so again we are putting a real value in or we're putting an amplitude here in our pot, these have been polar coordinates, uh, where we put a real value here and it should come back and say that the real value here dampens this expansion, so it ends up multiplying this. the effect is to multiply this function here by an exponential of the inverse slope so that the overall signal resulting from doing that does not grow and is finite and again you can see more in the video about the Laplace convergence region. transform in the case of the z transformation is in polar coordinates and you will see that there are circles, there is a unit circle uh inside and you get another another circle, let's say inside the unit circle, so let's say it was one and then again you get a region of convergence uh that goes from uh where the poles are uh and outside of that and so again for all of these values ​​that are in the shaded region you would get a convergence of your z transform and so again when you see In this image, you should be thinking about a transformation located above of this, on top of this plane, where again, if you take this twist, place it on top of the plane and you can see now that it wraps around a circle in this complex plane, so this and this is another one. way to visualize the fact that these basic functions repeat because if we take this function here and flip it vertically and wrap it around the unit circle, once you've rounded to two pi, you'd be back at the beginning and So you'll go around and around this unit circle here with the transformation coming off the page and you can see that once you go around two pi you go back to the beginning and that's another way to visualize the repetition of the The base works in discrete time, like this I hope this has given you more information about the relationship between all of these different transformations.

If you find it useful, please like it. Help others find the video. Subscribe to the channel to watch more videos and check. As I've said several times, check out the links in the description below the video where you'll find links to all the other videos with more details on each of these transformations and there's a web page there with a full list. of all videos on the channel in categorized order