Feynman's technique is the greatest integration method of all time

There's a good

integration

here and by good I mean it looks hostile at first glance, but it turns out it has some really elegant solution development and the solution development here involves my favorite

integration

technique

. I'm talking about the Feynman approach of differentiating under the integral sign, so let's call our integral I and we're going to define an integral function I of some parameter a and where exactly we place this parameter. A sensible choice here would be as part of the argument of the sine function, so have e to the power of negative x squared multiplied by the sine of a x squared divided by x squared DX and the reason I call it sensible is because if difference partially with respect to a the sine of ax squared you get the derivative of the sine function as a cosine function, then you have the cosine ax squared and because of the chain rule, the derivative of a with respect to a is one and x squared it's just a constant multiple because we're taking the partial derivative, so we have this extra factor of x squared that's going to cancel out pretty well with the denominator, so yeah, this is a good option.

Depending on the approach, we are going to differentiate the integral function with respect to the parameter a and the golden question here is whether we can make the change. of the integration and differentiation operators, if we look at the integrand, here it consists of a Gaussian term e raised to negative x squared and we have a bounded sine function and all of this is divided by x squared, which is an increasing function. in this interval then we are dividing by an increasing function or we can say we are multiplying by Decreasing Function One by x squared so yes in this interval there are no problems related to convergence or bounding so yes we can make the change. upward and due to the upward shift, the total derivative with respect to a becomes partial, so we are partially differentiating with respect to a and the negative x squared

time

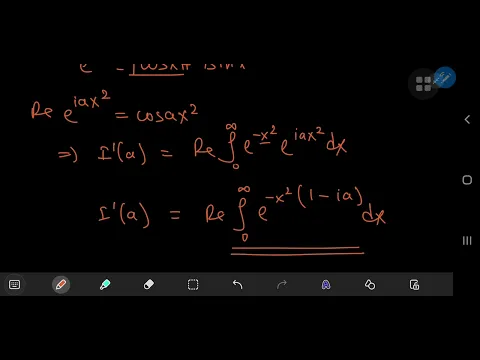
s the sine of a x squared divided by x squared and we are taking perform the integration with respect to sine function which is the cosine function, then we have the cosine ax squared and because of the chain rule we need the derivative of the argument which in this case is classified as x squared and this multiple of x squared cancels out quite well with our denominator here, so this implies the derivative of I with respect to a is the integral from 0 to Infinity from e to negative x squared

time

s the cosine of ax squared DX next we are going to make use of Euler's wonderful formula by which we know that e a i x is equal to the cosine of x plus I multiplied by the sine of If we need the cosine a x squared, then this means we need the real part of e a I a negative x squared multiplied by e a I a x squared DX so, when you multiply these two exponentials, you are left with the real part of the integral from 0 to infinity of e.

I'm going to factor out a negative term of generalized Gaussian integral where if you have the integral from 0 to Infinity from e to the negative s x squared DX where s is a complex number with a non-negative real part and in this case we have a non-negative real part, we have a real part equal to one , so anyway this integral sorts half the square root of Pi times S, which means we have a pretty good structure for I prime, we have I prime of a being equal to this half factor, then this factor of square root pi multiplied by the real part of the reciprocal of the square root of its complex number, which in this case is just 1 minus I times a and we can write this as half the square root of pi times the real part of 1 minus I by a to negative one half and now that we have the derivative of I with respect to a completely in terms of the parameter a alone, we can proceed to recover our integral function I from its derivative by integrating with respect to a, so on the right hand side you have square root of Pi times 2 times the real part of the integral of 1 minus I times a to the power of negative half d a, so this implies that on the left side you have I of a equals the square root of Pi times 2 times the real part of 1 minus I times a to the negative half plus one is just the right half and down again you have this half factor and you have to divide by the derivative of 1 minus I times a with respect to to the right which is just a negative I , the imaginary unit.

Okay, so we're dividing by negative I and we have this constant of integration that we'll also discuss later. Well, finally we have I of a equals the square root. Pi times two and wait a second, these factors cancel out pretty well once again, so we have the square root of pi times the real part of one minus I times the square root of that divided by negative. Now the good news is that we know that uh 1 times I equals negative I, which is just incredible. I mean, I think this little equation here is incredibly beautiful and another of the many reasons to love complex analysis, so we know this and we can write negative I as the reciprocal of negative I. just old I then we need the real part of I multiplied by the square root of 1 minus I multiplied by a and we have this constant of integration as well, so how exactly do we calculate the value of the constant of integration?

Remember that your integral function I of a was defined as the integral from 0 to infinity of e to negative x squared multiplied by the sine of a x squared divided by x squared, so if you enter an equal to zero, that means that above you have the sine of 0, which is zero, so the entire integrand collapses to zero, which gives you that I of zero is equal to zero, so that's pretty useful information, so using a equal to zero we have zero equal to the square root of pi multiplied by the real part of I multiplied by the square. root of one minus zero, which is anyway one plus the constant of integration we're looking for and the real part of I is zero anyway, so this implies that your constant of integration is conveniently zero.

Well, that means that we can finally turn our attention to our objective case and our objective case is that of a equal to one, so this implies that its objective integral, which is I of one, is equal to the square root of pi multiplied by the real part of I multiplied by the square root of 1 minus I multiplied by and a in our case Target is just one, so now we are interested in the real part of this complex number, which is quite easy to extract . All we have to do is use the polar representation of complex numbers, so let Z be the complex number. one minus I and in the polar form for that you need the module of Z which in this case is the square root of 2 and the argument of Z and remember that we are only interested in the main branch so here we have the inverse tangent of the imaginary part of the image that is negative divided by the real part which is the one that is classified as negative pi times four, which means that in the polar form you have Z equal to 1 minus I equal to the square root of 2 times e to the power of I negative multiplied by pi times 4.

And we're interested in the square root of 1 minus I and the square root is just an exponent of uh half, so this implies that the square root of 1 minus I is equal to the root square root square of 2 times e raised to negative I I Pi times 8 from time to time we are interested in multiplying the square root term by the imaginary unit I so performing this multiplication and expanding once again the complex exponential using the wonderful formula from Euler we have the square root of we have I multiplied by the square root of the square root of 2. multiplied by the cosine of negative pi times eight is the same as the cosine of pi times 8 because the cosine is an even function, so On the contrary, sine is an odd function so the negative sign just appears, so you have negative I multiplied by the sine Pi times 8. and multiplying this I term here, that gives you I multiplied by the cosine term and I multiplied by the cosine term sine, now negative I squared is just positive, okay, great. so finally we have I times the square root of 1 minus I and we need the real part of this and it's pretty clear that it's the square root of the square root of 2 times the sine of Pi times 8.

Okay, okay, this is Awesome, so all we needed was this real part multiplied by the square root of Pi and that gives you your objective integral I, so we can finally write here that the integral from 0 to Infinity of e to negative x squared times sine X squared divided by x. DX squared is equal to the square root of pi multiplied by the square root of 2 times the sine of Pi times 8. A really good result. I hope you enjoyed the video. Make sure to like and subscribe, thank you. See you next time.