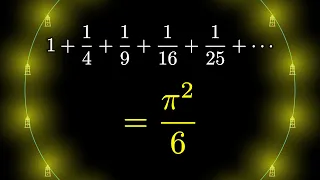Euler's real identity NOT e to the i pi = -1

Welcome to a new video from Mathologer. Anyone who watches these videos knows the Euler

identity

, e^(i*pi) = -1. But in

real

ity that is not Euler's

identity

. The mathematician Roger Cotes wrote about this as early as 1714, when Euler was only seven years old. In fact, I find it a little sad that people associate mathematician superhero Euler with a result that didn't come from him, rather than one of the many great discoveries he has made. Of course, it is very sad for Roger Cotes because he is not mentioned at all and no one has heard of him.

Anyway, I decided to make a video about Euler's true identity, the identity that made Euler a mathematical celebrity. It's this one here. Pretty strange, huh? It means that pi squared divided by six is ​​equal to the sum of one divided by the squares of all positive integers. This identity is a very surprising answer to the question of whether the infinite sum on the right adds up to something beautiful. Many of the best-known mathematicians of Euler's day had tried in vain to answer this question, so it was quite sensational when Euler found the answer in 1734. The fact that pi appears in the answer, without a circle in sight , of course, made the result very special.

The result is not pretty, but it is also important. Above is the definition of the well-known Riemann zeta function, the central function of the Riemann hypothesis, one of the most important unsolved problems in mathematics. What Euler managed to do was find the precise value of the Riemann zeta function at 2. Not only that, he also managed to do it for all even numbers. Now it appears that all of these values ​​involve the circular number pi. For example, this above is Zeta calculated at 4. and this is Zeta calculated at 6. To this day, no one knows if Zeta has good values ​​for odd numbers: 3, 5, 7, etc.

Euler was also interested in finding reasonable values ​​for the explosive sums you get when you try to calculate Zeta for negative values: 1+2+3+... you're familiar with that, right? In fact, he was one of the first, perhaps the first, mathematician to show that these sums are much more interesting than one might expect at first glance. Also watch my video on this mind-blowing topic, if you dare. Anyway, my mission today is to narrate and animate Euler's proof of his beautiful identities. Here we go. To begin with, it is not at all obvious that this infinite sum actually has a finite value, and if it has a finite value, it is a good value.

If you've ever looked at infinite sums, you may have come across a beautiful and strongly related infinite sum. It provides a lot of information in this regard, so let's warm up to this infinite sum. To achieve it, we rewrite the Euler sum like this. For example, we write 1 divided by 2 squared as 1/2 times 1/2. Make a copy and move the blue factors one term to the right. Now we have another infinite sum, which is also very good. Let's compare the two sums term by term. Well, in green we have 1 up and 1 down. Here the green parts are the same and the blue part below is larger.

Green the same, blue below larger, green equal, blue below larger, and so on. So the total below is greater than the Euler sum above. Now let's look at the brilliant method of calculating the sum below. We will first truncate this infinite sum at the fourth term and calculate the partial sum. Now get ready for some math magic. 1 times 1/2 equals 1 minus 1/2, funny, right? 1/2 times 1/3 equals 1/2 minus 1/3, and so on. Now we remove the brackets and we get a kind of pirate-type mathematical telescope. Let me explain that to you. Here is one of the segments of the telescope and here is another one, okay?

Now we slide the telescope: -1/2 plus 1/2 is 0, -1/3 plus 1/3 is 0, so our partial sum becomes 2 minus 1/4. Now we have truncated the infinite sum into this term here. If we had truncated it at this term, a longer telescope would have given us the partial sum 2 minus 1 hundredth. The more we truncate the sum, the smaller the number we subtract from 2. At infinity it disappears, so our telescope's sum becomes exactly 2. Okay, so these infinite sums can reach

real

ly good values, which is what Euler & Co. gave hope that the same would be true for the closely related sum they wanted to calculate.

Furthermore, this sum is greater than the Euler sum, so the Euler sum becomes a finite number, less than 2. And pi squared divided by 6 is in fact approximately 1.644, which is less than 2. So that everything looks good. Well, that was the warm-up. So how did Euler prove his identity? Well, it starts with the so-called Maclaurin series of sinus function. Most of you who have done any analysis are familiar with the fact that sine can be written as this type of infinite polynomial. No doubt Euler and his contemporaries were very familiar with this. To give a complete picture and show where Euler's idea for his proof came from, it is important to know how mathematicians derive this formula, which I will explain in a moment, but for now let's study the identity.

The sine function, of course, comes from circles, and therefore it is not surprising that pi appears in it in certain ways. For example, if x is pi, sine becomes 0, so we get this nice equation for pi, which is almost as nice as the Euler identity, right? Question for you: how can we use this equation to calculate better and better approximations to pi? If you have an idea, let us know in the comments. Well, let's say you suspect that sin(x) can be expressed as an infinite polynomial like this. How do you find those coefficients? Well, it's easy.

We simply take x to be 0 and sine to be 0, just like the sum there, which means a must be 0. Now let's find the derivatives for both sides of the equation. If you don't know what a derivative is, don't worry now. Here the derivative of sine is cosine, the derivative of a is 0, the derivative of b*x is b, the derivative of c*x^2 is 2*c*x, the derivative of d*x^3 is 3 * d*x^2, etc. Well, if we now take x as 0 again, we get 1 on the left and 0 on the right. So b must be equal to 1.

Now we do the same thing again, we find the derivative. set x equal to 0 and conclude that c is 0. And again, and again, and again and that gives us all the coefficients. So if the sine function can be written as an infinite polynomial, that's what it will be. That's where the Maclaurin series for the sine function comes from. This identity works even for all values ​​of x, but whether this is really the case obviously requires a separate test. Let me demonstrate how well this works by showing you how the partial sums of this infinite sum are increasingly better approximations of sin(x).

Here we go. Let's plot sin (x), there it is, and this first partial sum, which is just a line, the second partial sum is this cubic function, and we'll move on. As you can see, they wrap more and more around the sine function and for an infinite number of terms they match. So, as you've seen, the infinite sum on the right is formed term by term with derivatives of the sine getting deeper and deeper at 0. That's wonderful and gives us similar formulas for all kinds of known functions, such as the exponential function, cosine, etc At the same time, this method is different for getting the infinite polynomial than what most of us would try for finite polynomials, right?

For example, for a linear function like this, we could construct it using two points on the graph. For a quadratic function that passes through three different points. So it's pretty intuitive to see if we can determine that infinite right side with a similar method. And that is exactly what Euler does. He constructs the infinite polynomial in a different way, that is, using here these special points, which of course indicate the zeros of the sine function. Well, let's consider the middle three points. This part of the sine looks like a cubic function and we can immediately write a polynomial that has these three zeros.

There is. It's pretty clear that it has those three zeroes. Let's trace it. Well, it has those three zeroes, but other than that it doesn't fit very well. Of course, this is just one of the infinite functions of the cube that has these three zeros. We get the other one by putting a constant in front of it and changing it. Let's do that. Okay, go down, go down, go down, go back a little bit, and so we get a fitting function, when the slopes of the functions at 0 are equal to each other. It's not hard to see that happening when the constant is 1/pi^2.

Let's continue with that. First, a little cleanup work: put the constants in parentheses. Two ones out there, order the factors and combine the last two factors like you learned in elementary school. I hope you've been paying attention. Okay, it looks good. Now it is also easy to check that this cubic function, like the sine, has a slope of 1 in 0. Now let's do the same calculation for the 5 middle zeros. The polynomial we get then is a function of the fifth power and looks like this. As for algebra, we get exactly the same answer as now, with an extra factor.

This factor contains 2*pi instead of pi, for the outer zeros 2*pi and -2*pi. Now we do this over and over, adding two zeros each time. You see that the functions become more and more similar and in infinity they become the same again. So Euler now has two infinite polynomials that are both equal to sin(x), right? Now, since the infinite expressions are equal in some way, we expect to obtain the infinite sum when we evaluate the infinite product. Let's see how this works numerically, first for the infinite sum (that's what you get) and here the smallest terms you get when you calculate the first factors of the infinite product.

As you can see, you get a fairly good agreement between the coefficients, which improves as more factors are used. So this really seems to work. How do we now calculate the complete infinite product? Well, we work one factor at a time. Then mark the first two factors and multiply them and you will get this. Take the result and the next factor, multiply and you will get this guy. Now let's also highlight the term x^3, because it will be very important in a moment, and let's keep an eye on how it evolves. Well, there's the next factor.

Multiply and you get this, and again. Now look at the green part. It's pretty obvious what will eventually happen when you finish multiplying. The term x^3 will look like this. Now remember that the x^3 term of the infinite product made must be equal to the x^3 term of the infinite sum, so we get this equation here. Let's simplify. First multiply by -1 and then by pi^2 and voila, the true Euler identity. Quite an ingenious method, right? And all those other identities I talked about before, like this one above, are also obtained by comparing coefficients of the infinite sum and the finished product.

The previous identity is obtained by comparing the coefficient of x^5 in the Maclaurin series with that of the infinite product produced. You can also try this yourself. If you can do it on your own, it's really worth it. If you get stuck, I'll eventually do the nifty calculation in a separate video on Mathologer 2. Of course, there's a lot more I could say about this identity. I should especially emphasize that what I have shown is not a complete proof. Some work is still required to make this test comprehensive, but it is possible. However, what I have shown is practically everything Euler had when he decided to publish the proof of it.

Believe it or not :), he didn't have access to Mathematica, so all the numerical evidence supporting his proof had to be solved by hand, and he had much less evidence than I showed. It took Euler several more years after publishing his identity to find completely complete proof. Finally, let me mention two surprising facts about Euler sum. For my first surprise, let's look again at the way Euler writes the sine as an infinite product, up there. If we set x equal to pi divided by 2, the sine becomes 1 and when we rewrite the factors on the right as a fraction, this is what we get.

Solving pi divided by 2 gives the so-called Wallis product, named after the mathematician John Wallis, a very nice and useful infinite product, with squares of all the even numbers in the numerator and squares of all the odd numbers in the numerator. denominator. Very, very beautiful, don't you think? Surprising fact number two: many of you will be familiar with Leibniz's formula, this beautiful identity mentioned above. I found out about this recently, but Euler mentions in one of his articles that this identity can be achieved in exactly the same way as the Euler sum, the sum this video is about, by taking the function 1-sin ( x) as a product. write, using the zeros (that's pretty much all you need) and then the x coefficient of the Maclaurin series. comparable to that of the infinitely produced product.

It's not difficult with that information, so maybe one of you can leave the details in the comments. Oh, by the way, although this great identity is named after Leibniz, as is the Maclaurin series of all standard trigonometric functions, it was known to Indian mathematicians at least 300 years before Lebniz and Maclaurin were born, and there could have beenbeen discovered by the mathematician Madhava of Sangamagrama. Almost no one is aware of this or cares. How sad. Anyway, that's all for today. As always, let me know how well this video worked for you and until next time.