A tale of two problem solvers (Average cube shadows)

And not something specific like the state of a

cube

. Therefore, if we ask which of these two mindsets is associated with the discovery of new mathematics, then surely the correct answer must be a combination of both. But I would suggest that many people don't give enough weight to the part of the mix they want to delve into in the calculations. And I think there is a certain risk that the videos I make contribute to that. In my podcast with mathematician Alex Kontorovich, he talks about the often underrated importance of simply delving into mathematical processes to develop intuition, whether you're a student involved in a new class or a practicing research mathematician involved in a new field of research.

The science. Stay. In fact, one listener wrote to highlight the impression this particular section made. They are doctoral students and describe themselves as worried that their math skills are fading, which they attribute to being older and less sharp. But hearing a practicing mathematician talk about the importance of doing hundreds of concrete examples to learn something new clearly changed his perspective. In his own words, realizing this completely changed his perspective and his results. And if you look at famous mathematicians throughout history, Newton, Euler, Gauss, all of them, they all had seemingly infinite patience for doing boring calculations.

The irony of the bias toward manifesting ideas that allow us to avoid calculations is that the way people often train their intuition to find those ideas in the first place is by doing lots and lots of calculations. All that being said, something would definitely be missing without Alice's mentality here. I mean, think about it, how sad it would be if we solved this

problem

for a

cube

and never came out of the trees to see the forest and understand that this is a very general truth and applies to a large family of shapes. . And if you consider that mathematics is not just about answering the questions you are asked, but about introducing new ideas and structures, then one of the interesting notes about Alice's approach here is that it suggests an interesting way to measure the idea of ​​convexity .

Instead of just having a yes or no answer, whether it's convex or not, we can put a number on it by saying, think about the

average

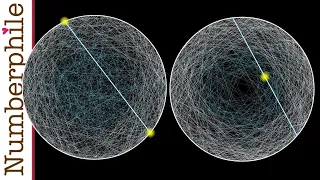
area of ​​an object's shadow, multiply it by 4, divide it by the surface area, and if that number is 1, you have a substance. A solid is convex, but if it is less than 1, it is not convex, and how close it is to 1 tells you how close it is to being convex. Also, one of the nice things about Alice's solution here is that it helps explain why mathematicians have what can sometimes seem like a strange fascination with generality and abstraction.

The more examples you see where generalization and abstraction help you solve a particular case, the more you will begin to embrace the same fascination. As a final thought for the loyal viewers among you who have been stuck on this until now, there is still one unanswered question about the premise of our mystery. What exactly does it mean to choose a random address? Now, if this sounds like a silly question, like of course we know what it must mean, I invite you to watch a video I just made with Numberphile about a probability puzzle known as Bertrand's Paradox.

After watching it, and if you appreciate some of the nuances at play here, your task is to think about where Alice and Bob implicitly answer this question. Bob's case is relatively clear, but the point at which Alice ensures some definite distribution over space in all directions, well, it's not clear at all, it's actually very precise.