What Is an Integral?

Let's say we want to find the area under this function in the interval 1 to 9. One way to do this is to divide the region into four segments and draw a rectangle inside each segment, so that in the upper right corner of each rectangle it touches the function the sum of the area of ​​these rectangles is an estimate of the area under the curve the estimate is obviously poor in this case because the rectangles simply do not fit under the curve they are too wide we can do better by doubling the number of rectangles once twice three times four times five times and six times until we have a total of 256 rectangles, these narrower rectangles fit better under the curve than the wider ones, so the sum of their areas is a much better estimate of the area under the curve. curve. curve, we could do this differently by placing rectangles on the four segments, so that the left edge of each rectangle touches the curve, then we could double the number of rectangles once, twice, three, four, five and six times, the result is the same. of rectangles that fit fairly well under the curve and provide a decent estimate of the area under the curve when adding the area of ​​the 256 rectangles, we could finally fill the four segments with rectangles so that the top center of each rectangle touches the curve . doubling the number of rectangles once twice three times four times five times and six times leads to the now familiar result that the rectangles fit best under the curve, allowing the sum of the area of ​​all the rectangles to give a good estimation of the area under the curve. curve, it doesn't matter if we position the rectangle so that the curve touches them at the top right corner in the center or at the top left corner, as long as they are narrow enough to fit well under the curve, they can provide an estimate of the area under the curve

what

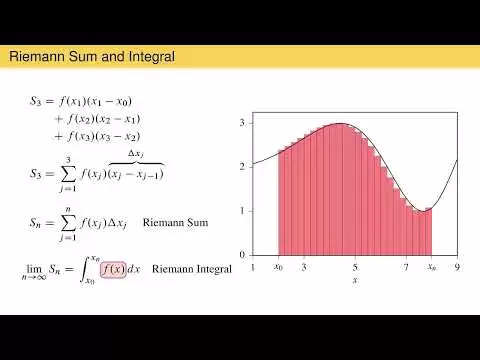
we would like to do is translate this concept into mathematics by looking at the same function again let's imagine that we want to find the area under the curve between these two x coordinates let's also imagine that we will estimate the area using rectangles within three regions of the same size to To translate this into mathematics we need labels for the x coordinates that define the range of each of these regions from left to right, let's call them x0 x1 x2 and x3 now let's place a rectangle between x0 and curve at x1 the area of ​​this rectangle is its height, which is the value of the function at x1 multiplied by its width, which is x1 minus x0 to estimate the area under the curve we must add to this the area of ​​the rectangle in the following region which is its height the value of the function at x2 multiplied by its width x2 minus x1 finally we need to add to this the area of ​​the rectangle in the third region which is the value of the function at X 3 times x3 minus x2 let's call this sum of areas of uppercase rectangles and give it a subscript of 3 to indicate the number of rectangles used in the sum.

This can be written more compactly using addition notation with the variable J as a subscript and taking values ​​from 1 to 3 the argument of the sum is the height of each rectangle the value of the function in X sub J multiplied by the width of each rectangle X sub J for the x coordinate of the right side of angle j3 minus the x coordinate of the left side of the same rectangle which is This means that X sub J minus X sub J minus 1 3 rectangles does not provide a very good estimate of the area under the curve from angle J 3 multiplied by its width and add from J equals 1 to an arbitrary value.

The number of rectangles in this is S sub n, a sum of the area of ​​n rectangles and is called the Riemann sum. The number of rectangles could be 6 12 24 or any other number, but S sub n alone becomes a good estimate of the area under the curve. If we take the limit of this quantity as the number of rectangles, the value of n tends to infinity in the limit of including many rectangles. S sub n is the area between the curve and the x-axis from X 0 to X sub N and is written symbolically as the

integral

from X 0 to X n of the function f of Riemann

integral

between two fixed limits sometimes called a Riemann integral in the integrand f of as the area between the curve and the x-axis in an interval, but this is only true if the function lies above the x-axis, for example, this function lies above the x-axis between x is equal to 0 and x is equal to a point 185 the Riemann integral in this interval is positive one point one to one and can be interpreted as the area under the curve in this interval because the function is never negative between x is equal to one point one eight five and three the situation is different because the function is negative the Riemann integral over this region is negative two point nine nine seven because the function is always negative clearly a real geometric area can never be negative and that is why we need to refine our definition of the Riemann integral.

A better definition of a Riemann integral is that it is the net area between the function and the x-axis in some interval, understanding that the areas below the x-axis are negative. and the areas on the x-axis are positive only in the case where the function is always positive. Can we interpret the Riemann integral as a true geometric area, otherwise the value is a net area? Until now we have talked about definite integrals that are between fixed limits and that are written as the integral from A to B of a function multiplied by a differential width where a and B are constants, these integrals have been defined in terms of Riemann sums with a geometric interpretation that is useful but does not provide a practical solution.

One way to evaluate integrals is provided by the fundamental theorem of calculus, which we'll get to in just a second. If we replace the upper limit B with the variable X we obtain the integral from a to X of the function multiplied by a differential width. The result is no longer a value, but the result is a function of of integration and it could be anything that you t WX and so on the function f of U is the function f of X with The calculus states that the derivative of the function capital f of X which is the result of an indefinite integral is equal to the integrating function small f of of differentiation this provides an immediate way to find the indefinite integral of a function determine which function when differentiated gives the function you are trying to integrate, for example,

what

is the integral of the cosine X the function that when differentiated gives the cosine X is sine a comprehensive one.