Edward Witten | Knot Invariants From Gauge Theory in Three, Four, and Five Dimensions

well today we start a new group of conferences organized by cmsa and chiang mai university together and there will be 10 more uh conferences in the next few days and even in January and um well uh we invited uh juan jones to give a talk on a couple of ago of months and well of course we were very sad to hear that he actually passed away a couple of weeks ago and we organized some lectures in memory of one, so Cliff will be the chair of this written talk forever, so let's get started, yes, thanks, so what is it?

I'm going to introduce you to speaker Edward Whitton. I imagine anyone who hasn't been living on Mars or socially isolated for the last 50 years knows who Ed Whitton is. Thinking last night about you know what to say and thinking about this, the history of Gage's

theory

, it occurred to me that behind every

theory

committed to advancement there is a fundamental article by Edward Whitten, I mean, essentially from the beginning, starting with the first. know the solutions in r4 for the dual equations of yang mills and then, you know his influence with a tia bot and a singer, you know the florida floor, based on his homology theory in the super symmetric quantum mechanics article by ed whitten and then of course written cybernetic equations, pushed and written equations, written vapor equations, bromoph whitney and variance, and then the whole history of topological quantum field theory, uh, quantum spin, Simon theory, quantum map theory um, you know all this stuff, um, you know the profound influence of uh,

edward

whitten.

So anyway, having said that, I'm very happy that you asked me to present it and the title of it is non-invariant

gauge

theory in

three

,

four

and

five

dimensions

. Thank you very much, Cliff, and also yes, for the kind words. You're going to hear that the Jones polynomial of a is not going to be an important ingredient in my lecture, so the Jones polynomial was a pretty extraordinary discovery that von Jones made in the early 1980s, where he went from questions and von Weiman algebras to problems. into things related to integral lattice models of statistical mechanics in two

dimensions

in a quite extraordinary way and invented this new type of one-

knot

invariant, the Jones polynomial, as you will hear later in the talk, I became interested in several more years Later, actually, largely thanks to the influence of Michael Tia, I will mention some of the other developments during the talk and the Jones polynomial has been studied by both mathematicians and physicists from an extraordinary number of points of view since it was first developed. invented, which was about 1983.

So we are all very sorry that von Jones is not with us today. In fact, you heard an earlier version of the lecture I'm giving today because we and Cliff also visited New Zealand last winter for a few weeks. We were able to enjoy mathematical discussions with Vaughn and also a little introduction to some of his favorite New Zealand pastimes, but it's pretty sad that he's no longer with us, so I'll continue with this lecture where you hear a bit about a physicist about the Jones polynomial and just some of the things that came after; There are too many for a single lecture, so I will explain the relationships between a sequence of theories in two,

three

,

four

and

five

dimensions in two dimensions we will have what are called the conformal blocks of the wzw model in three dimensions there is the Jones polynomial and its Related to Churn Simon's gage theory in four dimensions is the Super Yang Mills theory and in five dimensions we will have a candidate for the categorization of the Jones polynomial or, in other words, a candidate for a refinement of the Jones polynomial that is called covalent ophthalmology of a

knot

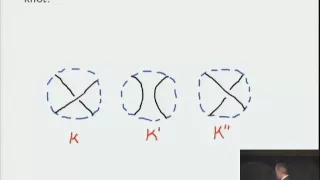
, so the Jones polynomial is a rather subtle invariant of a knot in r3 like the i' I have outlined here and since his original work, his constructions have generally been related to mathematical physics in a variety disconcerting shapes.

Jones himself gave several related constructions of the Jones polynomial. The one I'll mention today involved depictions of the Jones braid. grouping a braid in a mathematical sense is an image like this, so in this it is intended to be a three dimensional image projected onto the plane, time runs vertically and at any given moment you have a two dimensional plane with points on it. four points in the case I have drawn as time goes by the points move and to make a braid they move freely without crossing each other and then they return to their initial points so images like this are a braid with four strands.

Images like that form a group and can be composed by gluing one braid on top of another, so if I have this braid and another similar braid, I would literally put the second one on top of the first, glue the two images together and the topological classes. of such images or homotopic classes or such images then form a group, so Jones constructed some rather mysterious looking representations of the group of braids, the representation matrices depended on the complex parameter q, so I will call them r sub i of q where i tag the particular jones. representation and for each i the matrix representation also depends on q, so the precise number of these representations depends on the number of strands considered, for example I think for four strands there would be only two representations, one of Jones's original definitions was the following First, you can tie a knot by gluing the top and bottom ends of the braid rope.

Just take the top four types here and the bottom four here and glue them together, say pulling, pulling out of the page towards me and then glue it back to the bottom to glue the top to the bottom without introducing any crossovers or intersections and that turns a braid into a knot or, in general, what is called a link, a knot is the embedding of a single circle. in r3 a link is the case of possibly more than one disjoint circle, now gluing the top to the bottom is a bit like taking a trace, so perhaps it suggests that it is natural to take the trace from the representation matrices of the representations of Jones, so what is Jones?

What I did was the following: let's assume that b is a braid and that the curl i of b is the matrix that represents this braid in the representation r sub i, so I have demoted the complex variable q to a subscript here and now we think about the main argument. of the representation matrix is ​​the choice of degree, it is an n by n matrix for some n that depends on the number of strands and also on the choice of representation i, so one of Jones's essentially original definitions is that a a certain linear combination of these traces is the Jones polynomial, so there are certain functions ci of q that you must include and a linear combination of traces with these coefficients is a representation, it is an invariant of a no and that variance is called a polynomial of Jones of no.

Now everything about this formula is somewhat mysterious first, the construction of the representations of the jones braid group was not obvious, second, the particular functions ci of q that you have to use were obscure and perhaps more important because the same knot can be constructed as trace of many different braids It's not entirely obvious why traces of representations of groups of braids are a good approach to achieving non-invariance, so I learned about all this stuff for the first time about five years after Jones's original work thanks to mike latia. You predicted that the mysteries should be unraveled by playing jones. polynomial in quantum field theory there was a very important step taken by the Japanese mathematicians Tsuchiya and Kanye, they demonstrated that the Jones representations are those that arise when the correlation functions of a two-dimensional conformal field theory known as the wzw model are decomposed in conformal. box a decomposition that was originally analyzed by a kinetic enzyme, well logical, the wzw model is a two-dimensional conformal field theory that depends on the choice of certain data, a compact symmetry group g and a positive integer k can be generalized to non-groups compact, but then the theory is much more complicated because today we consider a compact symmetry group g and then the model also depends on a positive integer k it turns out that in relation to the Jones polynomial g should be its 2 and k should be related to the variable q used by jones by this formula here an integer k corresponds to q being a root of particular primitive unity the wzw model has what are called primary fields in various representations of g to make contact with the jones representation we consider a primary field madness in the two-dimensional representation and then we look at their zero-gen correlation functions, so to define them we take a zero-gen Riemann surface, a sphere like the one I've drawn here, two spheres, then we take some points on the two spheres that i' We have labeled z1 z2 through z5 in this image and then in physics language we insert the primary field phi at each of these points and then the model w produces a function that physicists know as the expected value of this product of the operators i' We have written the operator as phi of zz bar where the notation is only intended to tell us that these functions are real analytic functions but they are neither homomorphic nor antihomomorphic, so they depend on both the z bar and the z bar, but locally one could think that they depend on them. regardless of the z and z bars, which is what real analyticity means, as I said, these functions are not homomorphic, they are antihomomorphic and cannot be factored as the product of a homomorphic and antihomomorphic function, but conditionally consumerologists have shown that they are finite sums. of products of antihomomorphic homomorphic functions, so the correlation function is the sum of the finite set of alpha of a product of a homomorphic function multiplied by the antihomomorphic function.

These are homomorphic multi-valued functions, so fortunately you can do this decomposition with a given set. of multivalued functions, but these multivalued functions have monodromes, so for each n you can define a bundle of vectors v n over the configuration space of n points with the basis given by the f alpha. These are automatically flat vector packages with the f alpha understood. as coherently constant sections and the monograms of these homomorphic multivalued functions are the monodromes of a planar vector bundle, so its monodrome is when the points move, it has representations of the group of braids, a braid is the configuration space of n distinct disjoint points in the plane is a flat bundle in the space of n distinct points in the plane, in this case the bundle of five sections whose sections are the f alpha is a representation of the group raid the uniqueness of the correlation functions From the wz model implies that these representations are unitary, Tsuchi and Kanye's observation, to simplify it a bit, was that the representations that are obtained in this way are the Jones representations of the group of braids, so that was very important to me because, although Jones had used mathematical physics from the beginning, the mathematical physics he used was much more distant from the quantum field three and this was an interpretation of Jones' representations, although not of the Jones polynomial of a, not directly in terms of the quantum field three, as now understood by physicists at that time, the wcw model is purely two-dimensional quantum field theory with no particular connection to three dimensions, but the relation of the conformal blocks of the wzw model to the Jones representations of the braided group showed that the wzw model is somehow connected to three dimensions because Jones had related its representations to non-

invariants

and not in variance means topological invariance in three dimensions, in this case a topological invariance of a loop embedded in r3.

Now there were more clues in this period about the relations of the wzw model with three dimensions, but there really won't be time to explain them all, the most recent clue was the work of Eric Verlindi, who defined certain operators acting in the space of conformal blocks and their work also led to important work on conformal blocks by Moore and Cyborg, so a lot happened in this period. regarding the ingredients I'm talking about, but I won't give a detailed explanation of everything from that moment until now, if you want to relate the wcw model to three dimensions, there is actually a quantum field theory that depends precisely on the same. data like the two-dimensional wzw model, the data is a

gauge

group g which, for simplicity, is a compact group although it does not have to be compact and a non-zero integer k, we simply do Yang Mill theory in three space- time. dimensions with gauge group g, but we choose to make the action not the usual Yang Mills action but the Simon rotation function, so I wrote the trans-simons function of a gauge group in detail in terms of connection form with the components to sub there.

There are more abstract formsto write it the way I wrote it. It is not obvious that this function has gauge and variance properties because I have not expressed it. It cannot be expressed in terms of the curvature of angle f. In fact, it is invariant under gauge transformations that are homotopic to the identity but in three dimensions because because pi 3 I have been right, but only semi-illegibly in three dimensions and we run into a non-trivial homotopy group of the group of gauge g pi three of any The simple group e is z, so it is possible to have a gauge transformation that is not homotopic for the identity and it turns out that this function is not invariant, it is invariant under gauge transformations homotopic for the identity , but not under others, well, I hope I can clarify what.

I have done it, it turns out that this function is measuring a very mod variant 2 pi k times integers but it is not completely measuring the variant and the quantum reaction must be measuring the variant mod 2 pi k times integers someone is not muted, I think the argument The female path integral is the exponential of i multiplied by the action, so to make this value unique, the action must be well defined mod 2 pi multiplied by an integer, which is why k has to be an integer, which is an argument originally due to defecting even to Templeton and is somewhat similar to the argument showing that in the two-dimensional wzw model k has to be an integer, so that is part of the relationship between the two models.

Now the importance here of using the spin sign function instead of a standard yangmills action is that it can be defined on an oriented triple manifold w with no choice of metric tensor, we just don't use a metric tensor to define the action, we use a orientation to be able to integrate a triple form, but that is the only property of w that we can use, therefore the fine and path integral of this theory does not depend on anything except w itself; In other words, if it can make any sense, it will give an oversimplified topological invariant to w because there is what is called a framing anomaly, so you actually have to consider w as a three-frame manifold, but at the general level of Today's lecture we will not go into those details now we can include a no or an embedded circle k and w introducing what is known in quantum field theory as the Wilson loop. operator, the Wilson loop operator is simply the complete nominee of the connection a around not k, whose physics is correct this way and then you trace the entire nominee in some representation r, so the operator Wilson loop depends on an oriented non-k, so you know which direction to go when you calculate the integer and the representation r, so now we can consider the fine integral with an additional factor of this holonomy operator, so now it depends on w and not k and the representation and also depends on the small integer k in the action, but nothing else, so if, for example, w is r3, this will potentially give an invariant of a knot on r3.

Now I am going to establish the basic relationship between Simon's theory of 3D rotation and the 2gw zw model. If you want to study this theory with this action as quantum field theory, one of the most basic things you will want to understand is what is the space of physical states, what that means is that you take a spatial variety. Sometimes it's time to do a three-manifold, you quantize the theory and you want to get a physical state space of the system on that two-dimensional manifold, so to quantify any field theory you first construct the phase space, which is the solution space classics. will be a symplectic variety and you quantize it, in this case you will find that if you quantize the trans-simon theory, you learn that the physical state space of the 3d theory on some Riemann surface is the same as the conformal block space of the theory 2d on the same Riemann surface, so for example, as I said, let's quantize the three-dimensional theory on a Riemann surface sigma of genus g multiplied by r, where you could think of r as parameterizing time to construct the Hilbert space h sigma it has.

To quantify the appropriate classical phase space, the classical phase space in general is the space of classical solutions of the theory in sigma multiplied by r, but Simon's theory has the property that the classical field equation is simply f equal to zero, in other words, a critical point. of the Simon shift function is the same as the planar connection, the classical field equation states that the disappearance of curvature f is equal to d a plus a and j, so the classical phase space that must be quantized is the modular space of g beams planar about sigma, this can be quantified by choosing a complex structure in sigma which then induces a killer structure in m sigma, in other words, the complex structure compatible with its symplectic structure, a complex structure where the synthetic structure is positive type one and positive and then in such a structure you can quantize by looking at homomorphic sections, the prequantum line bundle in quantization is the kth power of what I will call l l is the fundamental homomorphic line bundle over m sigma which, in the case of a unitary group, it is called the determinant line bundle and the physical Hilbert space is the space of homomorphic sections of the kth power of l based on the modulus of flat or homomorphic bundles.

I have drastically shortened what is actually a long story, but the point is that the answer matches the well-known and for some people quite standard though also quite abstract description of the formal block space on a surface of genus g, so a lot People study the wcw model and its conformal blocks without being familiar with this description of them, but in other lines of work. uh, it's actually a standard description, for example, for people who work in geometric language. I probably learned this description from Graham Siegel, so like I said, this description may not be familiar to everyone, even if you're familiar with the WCW model, but it's widely used.

In some areas, the fact that the physical Hilbert space of three-dimensional theory is the space of conformal blocks in two dimensions is at least one way of saying well the basic link between two and three dimensions to obtain the Jones representation of the braid. group we simply take sigma as r2 or cp1 in a slightly different approach, but with parallel Wilson lines, in other words we take Wilson lines. Remember that a Wilson line is simply a no where we are considering the polynomial connection. A wink is an embedded manifold here, I take that embedded manifolds are, to first approximation, just straight lines running vertically in the time direction, we quantize in the presence of these Wilson lines and obtain a Hilbert space, but while the Well theory is A more thorough study of this quantization shows that as the points move we get a natural thick connection which is the same as the flat connection I described in the context of the wzw model and therefore a better way To say it is that when we quantize in with the presence of these Wilson lines we get not only a Hilbert space, we get a vector packet, the points could have been anywhere, so the Hilbert space is really the fiber of a vector package over the space of points and as the points move around what we actually get are the Jones representations of the braided group by quantifying the presence of these Wilson lines, then with some additional arguments you can get a formula for the expected value of a general Wilson operator on r3 that matches precisely the Jones formula for Jones representations, the Jones polynomial.

In terms of trails, maybe this is a good time to stop and ask if there are any questions. Oh, is it interesting? Yes, are there any questions? I don't see any, so go ahead, okay now in this presentation, since k had to be an integer. the theory is actually only defined for the integer k or in other words it is just to find a signal of this form which is a formula originally because tsuchiya and kanye were not studying the wzw model but only the conformal box k actually I didn't have to do it. be an integer and they had this general formula, okay, given, ask a question, there is a question, the question is the coefficients of c, yes, what is the interpretation in the context of two dimensions and three dimensions, they have this control , Yeah.

Okay, unfortunately I wasn't planning on explaining that, but c are related to the following: You consider a basic link in three dimensions where I have two knots but they are linked together and you could consider the expected value of that product in two dimensions. in three dimensions, so c can be expressed in terms of there being a well, at least in my opinion there are many ways to obtain these formulas, but my original approach involved a bit of surgery to relate a knot in r3 with a braid. I embedded the braid and that's twice a circle and then I did a surgery relating s2 times a circle to r3 which turned the braid into a knot and to do the surgery you needed to do a little calculation involving what would have happened with the simplest type . link and that calculation leads to these coefficients, so that was your interpretation, there are a number of other interpretations of these functions, okay, it needs to be explained really properly, it needs an argument that I'm not or at least I wasn't planning to do it.

Give today to explain exactly how you can go from the group of braids why you can go from the representations of the group of braids to um, not in variants, thank you, okay, I'll recap it a little bit, since a knot lives naturally in r3 but in the quantum field 3. Getting a trace usually means you have a circle times something, so you have to have a circle times s2 or r2 and then the braid is a set of points in r2 or s2 that propagates around the circle so that the configuration naturally leads to the traces of the braid group. but if you want a non-invariant you should be at r3 instead of r2 multiplied by a circle or s2 multiplied by a circle, so you have to investigate a surgery that compares s2 multiplied by a circle with s3 or r3 and when you do that surgery you end up with this formula, so I didn't plan to go into that level of detail today because I wanted to go into four or five dimensions, so in this presentation the theory is only defined for an integer k or, in other words, only for particular roots of unity . now, if you want the theory, it is defined on an arbitrary variety of three w which is believed to be the correct answer; in other words, the Jones polynomial of a that is not in r3 turns out to have an analogue for an arbitrary three-mountable w with or without a link. but this general analogue is believed to be defined only for the roots of unity, so as a physicist you say that it is naturally defined for these roots of unity, but well, but algebraically it can be defined for any root of unity. unit;

However, if one considers only the knots in r3, one can then what is obtained in this way from quantum field theory can be continued analytically from integer values ​​k to complex values ​​of k and hence the non-invariant is a function of a complex variable q and of course that's the way Jones originally presented it more specifically. jfq is not just a complete random homomorphic function, it is our own polynomial in q, so the

invariants

that jones discovered are described as non-polynomial, that is mysterious from the point of view of three-dimensional gage theory, but the interpretation in others The approaches make it clearer, so that was actually true in all of Jones's original approaches, but, for example, in terms of two-dimensional conformal blocks, it follows from fairly simple properties of the kinesic and zomlochikov construction that j will be a Laurent polynomial in q then the three-dimensional approach made three-dimensional topological invariants more obvious, but it did not give a direct explanation of why the invariants are a polynomial, but only invariants were defined on integers, so for a few 20 years I accepted the state of affairs that most well addressed, there were formulations of the Jones polynomial that directly explained why it was a polynomial but did not make the three-dimensional invariants obvious and there was John Simon's theory that made the three-dimensional invariants obvious but did not explain Why is it a polynomial?

It was a little frustrating, but I couldn't do anything about it, so I went on and thought about other things, but about 20 years later, new developments related mainly to what is called the volume conjecture motivated me to look for a new explanation why What The 3D shipping path integral for knots in r3 can be continued away from the integer k, so the volume conjecture is usually formulated as a statement that if you consider a representation of its 2 dimension, I think it is k plus 1 and you take k to infinity, then in the limit you get the exponential of the volumehyperbolic of a variety 3, assuming you're in it.

I've left out some details about what the limit is supposed to be, but if you formulate it, if you look carefully, you'll get I see that there is some analytical continuation involved in relation to what is physically natural anyway the volume conjecture was a fascinating statement without going into too many details. Relate the Jones polynomial and its analogue for variety 3 to the hyperbolic volume. The volume of the hyperbolic variety 3. So it was. I was interested in why this was true when I realized that expressing it in terms of physics fundamentally implies something I didn't know because it implies an analytic continuation away from the integer k.

One can almost, but not quite, formulate the volume conjecture in terms of what. it happens at integer values ​​of k, so understanding this turned out to involve a link between three and four dimensions that I think is just as interesting as the link between two and three dimensions, although it's not as well known yet, I don't think so before. I'm going to explain the story about the analog continuation of Simon's path integral. Let us briefly discuss the analytic continuation of an ordinary integral, so here is an integral in one dimension and it depends on a parameter a and I have called it z integral of.

Now, to prove the analogy between this integral and finding an integral, I'm going to derive a simple identity that will be analogous to this integral from what physicists call neighborhood identity in quantum field theory, which is why we learned the integral by integration Part by part. that the integral of d times dx of this of x multiplied by this expression is zero and that can be converted to show that z of a obeys a differential equation, so when we generalize the path integral we want to preserve the word identity, which in this case it means that we want to preserve the differential equation, so if you want to know in mathematical terms what the word identity means, there is a mathematical theory of what people call scan moduli, if you are familiar with that, a scan modulus is a set of knot invariants that obey the relations which are what I call here the word identities now to generalize the original integral we continue analytically from x to a complex variable z and then we can write the original integral as I did here where gamma is a cycle of integration which turns out to be the real axis, so we will generalize the integral by considering some other gamma integrating the same differential form over some other integration cycle.

Well, what kind of integration cycle can we use? Not a closed cycle. Use it because the integral will vanish according to Cauchy's theorem, in other words if we just integrate into a closed orbit in the plane oh sorry I was trying um oh sorry okay I'll try to keep talking while I try to find the screen I wanted share if we integrate in a closed loop in the plane, then we will get zero according to Koshi's theorem. Because I did not work? This will work, so we must choose an integration cycle with the property that the integral converges.

Are you watching now? If I could ask, you are not viewing the correct page. Are you looking at your desktop and are all your files there? Okay, let me. I don't know why you're looking at my desktop, but you can put the right file on the desktop if you open whatever you want to show in full screen, okay, okay, okay, I'm not going to try to write it down. A closed loop is useless because of the integral we are integrating. exponential of the homomorphic function, so the integral in a closed loop will vanish according to Cauchy's theorem, we cannot allow the integration loop to have a limit because then the word identity, its proof implies integration by parts, so it will fail , so the only option is a cycle that goes from infinity to infinity such that the integral converges, so, for example, there are two possible integration cycles here.

We could start it and end it on the positive or negative x or y axis, so I have presented it in one dimension, but it should be clear that we can treat an n-dimensional integral in the same way that we first continue analytically from real variables We consider an integral over a proper cycle at c n the properties you want for the cycle are as follows it has to be half dimensional and unbounded and the function minus the real part of f has to go to minus infinity at infinity along of gamma so that the integral converges for each gamma, we will obtain a generalization of the original integral and any differential equation that you can prove by integration by parts will be satisfied.

It turns out that there is a good theory of possible gammas given by Morse theory and this also provides a good framework for understanding the analytical continuation of such integrals, so what we wanted to do today. is to put the Simon path integral into the same framework, a quantum mechanical path integral in dimensions zero plus one can be studied in a very similar way, but for today we will only consider the three Simon path integral, so the Simon's path integral is an integral over an infinity. dimensional space u of all gauge fields a for the gauge group g the integrand is the exponential of a polynomial, so we are in approximately the same situation as before, there is no problem formally to continue analytically with the integrand, we replace by a curly complex value connection a a plus i phi where phi is a unique valued form in the gauge group, the gauge group is now the complexification of the original gauge group, for example we replace su-2 by sl2c and also the exponent of the path integral is a polynomial in a and we can We continue analytically with the same polynomial in curlier and replace u by the space u subs of complex valued connections.

The only drawback is that the integration must be performed over a medium-dimensional subspace of the space of complex valued connections, so we need to find a medium subspace. dimensional subspace we need to find a subspace that is of medium dimension and that has the property that the path integral analytically continuous converts, so how are we going to do it right? There is still a way to handle the first part, which is important in many areas of mathematics. and implicitly physics, although it is not always made explicit in physics in mathematics, for example, it is used in fluorochromology and many other things, so let u sub c be any set of fields in an upper manifold engine w whose limit is w , so schematically the picture is like this, here is w, is the limit of x, then, roughly speaking, choose any elliptic differential equation one x such that the desired fields in w can be interpreted as limit values ​​for a solution in x and defines gamma as the subspace of fields in w that are limiting values ​​of global solutions in x, so this subspace will be within a finite dimensional quantity of being half dimensional, the difference is given by an index, for example, suppose that w is a circle and u c is the space of complex-valued scalar fields phi.

First, let's hand pick a subspace of half dimension, do a Fourier expansion of the function and define gamma by setting half of the Fourier components to zero, say those where n is less than zero, but we can put this in our image, we consider the circle as the boundary of the unit disk in the complex z plane and we write z as r e i theta so now okay, here is our circle, it is the boundary of a disk x and we consider the scalar field phi as the boundary values ​​of a field scalar on x which I will also call phi and the elliptic differential equation that we choose is d bar phi is equal to zero.

A general solution can be expanded in powers of z with non-negative coefficients, so that when restricted to z equals one, what we had before with negative Fourier coefficients. vanishing, in other words, the boundary value space of the solutions in What we do is take w as the limit of a volt complex value, then we can use more or less any elliptic p but p is essentially uniquely or almost uniquely determined if we want the path integral to converge just as in the one-dimensional example we started with the path integral is in danger of diverge because after the analytic continuation the integrand of the path integral is no longer imaginary in the theory of ordinary transcendence, the i multiplied by something real is now in something complex, so the exponent has a real part that is not bounded above and therefore the integral is in danger of diverging, which we will save the day as an identity if we could write the exponent of the path integral as the integral of p squared something positive plus something negative then that would say that Although the real part can be positive in general, it is negative when p is equal to zero, so such an identity tells how dangerous the left side is not negative in general, but it is negative when p is equal to zero, so now it will be negative in our integration cycle.

If you are familiar with the supersymmetric band factory theory, when you look at the last slide you will see You might notice something: the negative term on the right side is part of the action of the n equals four super animals theory. You can think of the form we introduced as four scalar fields of n equals four, examining Will's theory topologically twisted to convert them into a form, the other two scalar fields have been set to zero in this formulation and the fermions of n are equal to the four-second theory and also the other two scalar fields are part of a more complete description of a path integral which is a topological invariant so related to the fact that the identity is linked in this way to n equals the force, you're being the theory of a thousand is that the equations p equals zero are supersymmetric equations for a twisted version of n equals the theory of four circular mills, in fact, Copston and I had come across these equations in our work on gage theory applied to geometric language, so we'll soon see why it's useful, but for the moment let's leave aside the relationship with super angle theory, so the picture is this: we have a variety triple oriented closed w for any choice. from a four-manifold solution of the equation p is equal to 0 at what's going on, instead of discussing spin sign theory, I wrote a simple integral that depends on an integer k, so we integrate on the unit circle in the complex plane this function k is an integer t is a complex parameter and this integral defines a Bessel function now if we do not want k to be an integer we can simply change the integration cycle we replace the integration cycle in the complex plane with the contour that I have indicated that comes from the negative relaxes and returns below, the negative relaxes and returns above the negative real axis, as long as t has a positive real part, the integral in this cycle converges and you can forget that k is an integer, of course you have lost something when k was an integer. we had a complete function of t in the original integration cycle this function is manifestly a complete function of t by changing the integration cycle we can forget that k is an integer but we lose something that we no longer have a complete function of t t had to have a positive real part to make the integral in the new cycle converge and we definitely change the analytic properties of the function, but we can move away from the integer k, so that's kind of what we've done in Simon's theory, the original integral was analogous to the integral on the unit circle k was an integer the modified problem that uses the format of what is like integrating in this other cycle where k does not have to be an integer but some properties are lost, so , what are we doing to obtain? moving away from the integer k is an analogue of this and if you ask what is lost and moving away from the integer k in this way, the answer is that we have to choose the four varieties x and that ruins the topological invariance of w because in general there will be no way to choose an x such that all difumorphisms of w extend over x, so we have realized a limited loss of topological invariancereducing ourselves to those differences of w that extend over some chosen x, but in exchange for that loss we have gained the fact that k does not have to be an integer, but there is an important case in which we do not lose anything and that is the case of the knots in r3 and that's basically because the knots in r3 are canonically well, r3 is conically the limit of a half-space in r4 and that doesn't really lose any topological invariant, so anyway, for the special case of knots in r3, it can be argued using Morse theory that all integration cycles are equivalent, so the standard integration cycle can be replaced by one for which k has no reason to do so. be an integer, so we get a new explanation of why John's polynomial, but not his prime, the three multiple variants can continue analytically away from the integer k;

However, due to the relationship with the superangle theory, we actually get much more: the equation p is equal to 0. It is a supersymmetric localization equation for n is equal to four superannual theories in four dimensions in other words the theory has a particular overload q that satisfies q squared is equal to zero such that if a topological field theory is made by passing to the chromology of q the integral in four dimensions is located in solutions of p is equal to zero, so This type of localization is the generalization of dorstromadekman, a tiabat localization in equivalent chromology.

It also has many applications in quantum field theory, so what I have said up to this point can be stated. In a more physical way, let x be a variety of four with limit w. We cannot preserve all the supersymmetry of n equals the four super flare theory when we formulate the theory about x unless x is flat, but even if x is not flat. We can choose particular couplings to preserve the overhead q, so we can assume that q remains a symmetry at any x and we also select a particular boundary condition along w, which is a subtle and important part of the story when doing so.

This, the claim is that n equals force here supremus on x gives a continuous analytic version of Simon's shift theory on w, so the analytic continuation of Simon's shift path integral on w is just a particular gauge theory path integral at x, the boundary condition we need has a simple description in In terms of string theory brains, it arises from a d3 ns5 system with a nonzero angle theta. It is actually a rather unusual boundary condition from the point of view of topological field theory. Not too unusual in the underlying theory of n equals four strip disputes.

It is a first-order boundary condition which is a standard elliptic boundary condition in second-order angle equations, but in localized theory in solutions of p equals zero, the boundary condition becomes trivial, it simply says that p is equal to zero along the boundary, so in twisted topological field theory this boundary condition seems very strange at first glance, it simply tells us to integrate over the infinite dimensional space of all solutions in x of the equation p is equal to zero. This boundary condition has an analogue in dimension two that was discovered by capostenan and orlov. Now step i.

I've described going from three to four dimensions as relatively non-standard, but once we take this step we can go much further using more standard arguments. First we apply electromagnetic duality to the four dimensional theory n equals four so in terms of brains doing something simple changes d3 ns5 to d3 d5 in terms of gauge three what happens is the following first the gauge group g is replaced by the gno dual of langlen group g dual for example sg2 is replaced by so3 but moreInterestingly, a symplectic group sp2n would be replaced by an orthogonal group so2n plus one, the parameter q of the Jones polynomial becomes e for i theta , where theta is the theta angle of gage theory, which means that an instantaneous field at the number n is going to be weighted by q to n, so the Jones polynomial, which was a polynomial at q, is the expansion of the Jones polynomial as an alarm polynomial and q will become an expansion in the contributions of different numbers of instants in terms of the bulk localization equations, nothing happens. the location is still in solutions if p is equal to zero, but due to the change from ns5 to d5 the boundary condition is completely different, now determine the elliptic boundary condition in the equation p is equal to an unusual elliptic boundary condition, as I will explain shortly because the equation and the boundary conditions are elliptic, it makes sense or at least will make sense if the compactness problems that have actually been aspects of which have been investigated in recent articles by talbs but which have not been resolved completely, but modular compactness issues can be expected to be resolved.

It makes sense to count with signs the solutions of the equation p equal to 0 that satisfy the boundary condition and then if an is the number of solutions of p equal to 0 with instantaneous number n that satisfy the boundary condition, the suprasymmetric localization will tell us that the partition function is the sum of an q to the power n and which will then be a dual formula for the John polynomial, in other words, the coefficient of q to the power n in the Jones polynomial is assumed to be the number an of solutions with number of insulin n that satisfy the limit. condition and if you ask what happened to the knot, the answer is that the knot is still there at the boundary and the boundary condition you should use in this description is the rather subtle boundary condition that depends on the knot, so the knot It is completely encrypted. in the boundary condition, then to get the Jones polynomial, the three varieties must be just r3 and x must be the four mountain vultures, r3 multiplied by a half line and we need a rather special boundary condition of boundary bounce, uh, the boundary condition that we have. need has all the general properties of an elliptic boundary condition, which means that with this boundary condition, for example, the sufficient operator p becomes a selfie for an operator with a discrete spectrum if you are on a compact manifold, for example, but it is constructed in an unusual way by requiring that the fields have a certain type of singularity along the boundary, so choose local x coordinates along the boundary and a y coordinate normal to the boundary so that the boundaries on y be equal to 0. and write the form phi as tangential part plus a normal part, the boundary condition is that the tangential part must have a singularity that I call nominal pole, it explodes as one over and when and approaches zero, where t is a standard set of generators from the algebra of su 2. i Call it nonpolar because Nam introduced this type of singularity.

Nam studied a one-dimensional analogue of these equations or a one-dimensional reduction of these equations which he used to construct monopolar solutions at r3 and in his work this type of singularity at the end point was important, which is why he called the singularity a non-survey. This is the boundary condition away from a knot and there is a refinement of this long enough along the knot, a more complicated type of singularity is required which I gained. In any case, I will not describe it schematically today, at least although I have not completely defined the boundary condition. This is a dual formula of the Jones polynomial with the new conjectural interpretation of the coefficients of the John polynomial as a learning series in q, but there is one.

The further step we can take from this starting point, we can categorize John's polynomial and obtain a candidate for one-knot kovan ophthalmology. What we get is closely related to the work of ghukov schwarzenwaffe, whose starting point was previously worked on by ugri and buffa. There are also a variety of works with somewhat related perspectives, for example a recent paper by meena aganajic from earlier this year in terms of brain categorization means replacing the d3 d5 system with a d4 d6 system starting with d3 brains activated for the collector x, the string is the one where you first replace x with x multiplied by a circle, but then you decompact the circle to the real line, in other words, instead of considering a d3 brain at by a circle and in topological field theory that does nothing more than then, if you replace the circle with r, it changes the image and you get categorization, as I just said, introducing the circle does nothing more than replace the circle with the real line non-compact that corresponds to the categorization.

Categorization means that you construct a physical Hilbert h space. Instead of purely numerical invariants, this Hilbert space is z multiplied by e classified by the non-numerical instant n and also by the fermion number f which in this context is given by the invariant eta patodi singer to d categorize what is done by taking a supertrace or index and that goes back to the Jones polynomial, so categorization means that in this context we construct a z multiplied by e the graded Hilbert base h, where z multiplied by the degradation is times the incident number n, the number of a gauge field at x is an integer n and then there is a fermion number. f which is given by the invariant eta singular atiya patodi of a field that satisfies the equation p is equal to zero and z multiplied by e the graduated Hilbert space has the property that a certain trace in it reconstructs the Jones polynomial the polynomial of Jones is a characteristic of Euler in this Hilbert space mathematically without mentioning brains what happens is the following remember that the Jones monomial comes from counting solutions of an equation in general, as far as I know, you cannot categorize the space of the set of solutions of an equation, however, according to Morse theory you can categorize the set of critical points of the function f the categorization of the set of solutions of df is equal to zero is the commonology of m the real deram chromology then if we want to categorize the Jones polynomial we want the set of solutions to the equation p equals zero to be the critical points of some function, that's actually not true on a generic variety of four and if you just look at the equation, p equals zero at At first, it won't seem true if I hadn't known that Kovanov and others had categorized John's polynomial.

It would never have occurred to me to try to write the equation p equals 0 as the equation for the critical points of something. If you know that John's polynomial has been categorized, then look it up. and you find that if the four manifolds the equation is schematically delta gamma delta phi is equal to zero for some gamma energy function that depends on all fields, the full set of fields occurring in the equation p is equal to zero, but this is a gamma that can only be defining for x of a particular type, not for a general categorization of four varieties means that you add another dimension by replacing x with y, which is gradient d phi dt is minus the gradient of gamma now for the categorization to work in this field theory context the gradient flow equation has to be elliptic generically if you take some local gamma functional of some fields you can always write first a gradient flow equation, but it is usually not elliptical.

I only know of a few cases where an elliptic equation is obtained that way and this is one of them, since it is elliptic it makes sense to count its solutions assuming that the relevant compactness problems can be solved, assuming that we can construct an analogue of fluorocarbology and this would be the categorization of the Jones polynomial. specifically it means the following the solutions of p is equal to zero in a variety of four x are the classical vacuums we make a Hilbert space h zero with a basis vector for each classical vacuum a classical solution has two integer invariants one is the instant the other number n is the invariant eta which in this context is an integer f because we have two integer invariants we get a z multiplied by e rating of h zero the physical Hilbert space is fine h nothing depends on no because they were not entered in the conditions of contour in this equation p is equal to zero, however, the physical Hubbard space is not h nothing but rather is the columnology of a differential or supercharged q that acts on h nothing the elements of the matrix of q between different vectors based on h nothing are calculated by counting the gradient flow lines between different critical points as is usual in the suprasymmetric approach of morse theory, so finally this is theconjectural image for a description of covan ophthalmology gauge theory of a knot in terms of counting solutions of differential equations in five dimensions and what is needed to make it rigorous is primarily an understanding of the compactness problems associated with the solutions of those differential equations, so we have online the expert on such questions here, namely cliff, so you can consider asking questions about cliff after my talk, so in summary, we have discussed the relationships between a string of theories and dimensions two three four and five in dimension two we have the conformal box of the wcw model and dimension three was the Jones polynomial and its description by Churn Simon's theory in dimension four we relate this with n is equal to four supreme theory and in the last step we go to dimension five, the categorization of the Jones polynomial or at least I suppose that is the last step.

I don't see any more steps to suggest, so I know that right now it's the last step, although some aspects of it can be well understood with some six-dimensional conformal field theory, four-gauge theory, as far as I know, the five dimensions are the last step, thank you, this is what I have to tell you, thank you very much, Ed, that is really an amazing image. We've grown up together here, so I guess we could answer questions. I have a question here. Someone is asking. Besides r3, are there three other varieties where the integer k can be continued analytically to a continuous variable?

Well, for any of the three w varieties, if you choose. an x with the limit w you can do this analytic continuation, not much is known about what you get in general, it will ruin some of the variance of w because what will curve will be the subgroup of morpheus tissue and w that extend over x. So, for example, if w is a three taurus, what could you take x to be x? It could be taking a circle in the three tauri, it's the limit disk, so three tauri is the limit of a disk multiplied by two tauri, but to do that you choose one. of the circles in the three taurus, so you broke some of the three symmetry for us, so you can do this, but usually you will lose with the three-dimensional symmetry.

It is not very clear what you will get, but I could say gukov and koas. I'm not going to try to list them because I would forget that some have in a different language and do not emphasize the 3 gauge interpretation, but with a different approach to this brain system, I have investigated some of what you get with three other collectors, but in En Overall, I would say it's in its infancy, not much is known, so we have another question which is, what part of the chain of reasoning is broken if you try to categorize by going to a d uh 5d7 system?

This is from arnav, well, it was It was a miracle that we got a five-dimensional Olympic equation, I think so. I don't know of any natural elliptic equation above five dimensions. We should try to get it, but okay, the link to the Joneses, but look, okay, I think the question is like this. polynomial analytically we continued to put d3 and s5, that's why we had to do it. We were in three dimensions with John's polynomial so there was an important three so we had to use d3 and s5 and then we were lucky that the duality of s then can s5 to d5 so we had a dual description by d3 d5 so we can raising it d406 the question I think the question is by raising d5 d7 more, would we get something interesting?

I'm not going to answer that question now, but I'm also not going to tell you what we get, that's interesting. I haven't been able to see how to get anything interesting by going to d5d7, but I'm not going to say that you can't get anything interesting in five dimensions, yes, I think it's better. stop there, okay, in five dimensions you get this nice elliptic equation, if you try to go further you have to think of something new to do, that's why there's a question mark here. I can't suggest the next step, but I'm not going to say it.

I'm sure there isn't any, thanks, um, we have more questions, uh, Arnold, again, why did you lose topological invariance for your analytically continued general three-manifold plus the Lincoln variance? Your argument for going from 3d to 40 was going from w to x such that the limit of extend yes, yes, okay, that's a good question and it points to something I touched on lightly in the lecture, so if we do w multiplied by r plus, since it's not compact, we'll need a flat connection, we need a boundary condition in infinity in our plus and I'm hesitating because it won't be obvious why.

We can't just take the trivial thought connection as the boundary condition, so okay, I'm hesitating, I'm not absolutely sure what will happen if you try to take the trivial flat connection, take a generic, if you take a typical thought. connection at infinity in our plus, of course, that again involves a choice, so it will break the topological invariants on w, but I'm just not sure what will happen if you try to take the trivial fat connection to preserve topological invariance, I think that I should leave it at that, I might be forgetting something, well it will matter a little, it will be better if the trivial thigh connection is insulated, which it will be for many three varieties. so if you have a three mount fold where the triple 5 connection is isolated, you can try continuing with the trivial fly connection at infinity as the boundary condition.

I don't want to make any promises about what's going to happen, there are a lot of things here most of which haven't been investigated another question from andrew nicus does your categorization of the Jones polynomial shed any light on the volume conjecture? Some limit of the Jones polynomial of color of the knot and the three spheres would give the volume of the complement of the knot well, I didn't see the categorization it helped with the Jones with the volume conjecture um, the volume conjecture to be honest, I don't understand from a physical point of view why the volume conjecture should be true, the volume conjecture was part of my motivation to figure out how to continue analytically away from the integer k and relate, ultimately, that became the relation of three to four dimensions, but I didn't learn in that paper why the volume conjecture had to be true, all that happened was that I defined an invariant integer with the property that if that integer is nonzero for a given no, then the The volume conjecture is true for that no, but I didn't discover any reason why the integer in question would be non-zero for every no, so I don't even know how strong the evidence for the volume conjecture is to me. , if you study 100 hyperbolic knots, maybe you will find one where the invariant is zero and the volume conjecture is the default for that knot, but maybe the volume conjecture is true, if it is true, it definitely is. true for a reason I didn't discover there are other questions hey well here we have a question august in mourinho I have three questions about logan mentions one what's left of the additional fields of n equals four in the original term simon theory, that's your first question , uh, they disappear, uh, so okay, the extra fields form a machinery, well, the extra ones if by extra fields you mean the fields that I didn't include in my lecture, two more scalar fields and a bunch of fermions. goes into some machinery that is needed to make the four-dimensional pathogen a topological invariant so that you can apply localization to it, but when you apply localization, they disappear and you are left with the second analytical continuous three-dimensional integral question after taking electromagnetic duality, can you go back to three dimensions?

As far as I know, the answer is no, okay, you can do it right, so when you are in four dimensions, you have this twisted supersymmetric theory, you can try to localize it before the localization of electromagnetic duality. tells you that it localizes to a three-dimensional continuous analytical path integral, but after electrical reality localization it only tells you to count the solutions if p equals zero and you get no advice on how to give a three-dimensional interpretation of that for that As far as I know, the post-duality image is in four dimensions, you can go up to five but not down to three, as far as I know, okay and then the third question, can you analytically continue the relationship between Chern Simons and WGW, then?

An example of what that question would be specifically is: can we, then, Jones' representations of the braided group? We see them in turn, Simon's theory of the integer k, but Jones constructed them in terms of a complex variable k or called it q, so it is an example of the question would be: can we see? Can we do something with four-dimensional integrative theory to see continuous representations of the braid group? It makes a lot of sense that you could do it, but it's not something I've really done, yeah, I think. makes a lot of sense, what comes to mind is that the degree group involves points on s2 and then you have r, which parameterizes how the braids move, it has to be the limit of a four mount volt, we could take s2 as the limit. of a ball multiplied by time, then that could be our four-man volt and then the data on the four mountables at time 0 would be a ball with on its limit the end points, it makes a lot of sense that when studying that you would see the jones non-whole k renderings, can't say I've tried to think it through though, thanks, so I guess I don't see any more questions, so I guess we can all virtually thank speaker Edward for his uh, wonderful talk, thank you very much, yeah , thank you so much, that's a great talk, thank you, great, seeing you all, good luck to everyone and I know it's safer in Beijing, but anyway, everyone, what a bye?