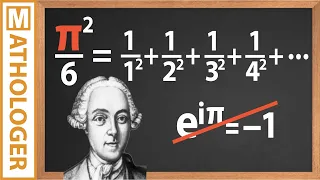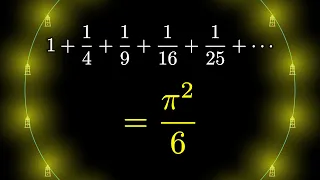Fermat's Christmas theorem: Visualising the hidden circle in pi/4 = 1-1/3+1/5-1/7+...

prime number like 17. Well, a prime number has only two factors, the good 1 and the prime itself. So what if the prime number is good in itself, as in the case of 17? Then we have good - bad equals 2 and therefore our

theorem

guarantees that every good prime can be written as a sum of two integer squares. Good? On the other hand, if the prime number is bad like 11 and then good, bad will be equal to zero. So our

theorem

says that bad primes cannot be written as the sum of two integer squares. And that is known as Fermat's Christmas theorem: good primes can be written as sums of integer squares and bad primes cannot.

This is also why I previously labeled odd numbers as good and bad. Now, Christmas in the name of this theorem is standard, although the connection with Christmas is quite tenuous. It derives solely from the fact that Fermat wrote about this theorem in a letter to the mathematician Marin Mersenne on Christmas Day in the year 1640. Still, if you are a desperate Mathologist, like me, looking for a Christmas hook, you take what you can get. get. And there's also a twist on the Christmas hook. Yes, you guessed it. Fermat's Christmas theorem is not Fermat's. The theorem was actually first stated by mathematician Albert Girard 15 years earlier.

And that's a photo of Girard there. Well, it's not actually Girard, it's cartographer Jodocus Hondius, which is what Google spits out when you ask about Girard. In fact, Google choosing some designated replacement when it can't find the right portrait seems to be as common as theorems being named after the wrong person, and sadly, as for Madhava, no Girard image seems to have survived. In any case, neither Fermat nor Girard provided a proof of the theorem and the first to publish one was Euler. Well, it's always Euler, right? Actually, while we delay proving the Christmas Theorem, it is worth mentioning another reason why the theorem is now so famous.

In 1990, mathematician Don Zagier came up with an absolutely incredible proof of the Christmas Theorem in one sentence. There it is, but good luck with that sentence. Figure it out and you'll probably be ready to start a PhD in mathematics. Now, historically, the Christmas theorem preceded our theorem 4 (good - bad). The 4 (good - bad) is known as Jacobi's two square theorem and, wonder of wonders, it appears to have been first proven by Carl Jacoi and, yes, that is Jacobi. And now we will prove the Christmas theorem and the Jacobi theorem? No, sorry, definitely not today. Mathologizing these theorems and making them truly accessible is very complicated and is still a work in progress.

But if I still can't give you the proofs, I would like to end today by mentioning at least a couple of simple and beautiful ideas that will give you an idea of ​​where these theorems come from. The first thing to keep in mind is that the bad half of Fermat's Christmas theorem is really easy. In fact, it is easy to show that not only bad prime numbers but all bad odd numbers cannot be written as the sum of two integer squares. None of these types up there can be written as the sum of two whole squares.

Since it's so easy to prove, let's do it. First, notice that every bad odd number has the form 4k+3, right, 4 times 0 plus 3 is 3, 4 times 1 plus 3 is 7, and so on. On the other hand, good odd numbers have the form 4k+1. In other words, good odd numbers are the integers that leave a remainder of 1 when you divide them by 4, and bad odd numbers leave a remainder of 3. What other remainders are there when dividing by 4? Well, of course 0 and 2 correspond to even numbers. So each integer is one of these four types. Now let's see what types we get when we square integers.

Obviously, the square of a number of type zero returns a number of type zero. And it's easy to see that squaring a number of type one also results in a number of type one. It just expands, right? Do you see the pattern? So now squaring a number of type two results in... no, not a number of type two :) Did I fool you? In reality, squaring a number of type two results in a number of type zero, as you can also easily check by expanding. And finally, squaring a number of type three results in a number of type one.

So, in summary, an integer squared gives type zero or type one, but then what are the possible types of a number that is a sum of two squares? Well, effectively, you're adding a couple of zeros or ones, so the sum of two squares can be something like 0, 1, or two, but there's no way to get to that 3. In other words, it's neither bad nor integer. . It can possibly be written as the sum of two whole squares. And that's the easy half of the famous Christmas theorem. Pretty easy, right? What else can easily be said about the proofs of our two theorems?

Well, not much, but one aspect worth highlighting is the identity up there. That identity that the ancient Greeks already knew is the glue that holds the two theorems together. What this identity tells us is that if we have two integers that are the sum of two integer squares, then their product is also a sum of two integer squares. Do you have an idea how this could work? Since all positive integers are products of prime numbers, once we know exactly how prime numbers can be written as sums of squares, there is some hope that this identity will allow us to extend the results for prime numbers to all numbers. integers and, in fact, also counting the number of ways to represent integers as sums of two squares, which is what Jacobi's theorem is all about.

And this is indeed what happens. Of course, as always, the devil is in the details. But I will leave those diabolical details for a while in the hopefully not too distant future. The big demon killer I'll want to use is the law of quadratic reciprocity. Some of you will be aware of the challenge that matologerizing will pose. Okay, and that's all for today. Just one more thing. If you liked what I did today, there's also a really nice video by 3blue1brown where he animates a

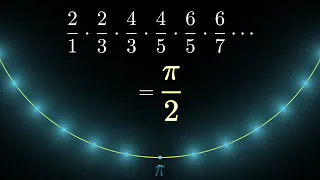
circle

-based proof of the famous solution to the Basel problem, that infinite series of pi over there.

And while you're there, maybe also check out Euler's original solution that I cover in the video at the bottom. Okay and that's really all for today and all for this year. See you in the new year, Fröhliche Weihnachten. Actually, actually, one more last promise. We recently hit 500,000 subscribers, which I think is pretty amazing for a hardcore math channel. Anyway, I think it's great and I'd like to thank you all for your interest and support over the years. I don't care about money at all, so I've always avoided even thinking about monetizing these videos. However, maybe next year will be a good time to take Mathologer to the next level and hire someone to help me edit the videos, prepare the subtitles, etc.

To prepare for this, I recently monetized videos by turning on the least annoying ads on YouTube. I also just published a Patreon page. If you enjoy these videos and can afford it, consider purchasing one of the memberships or making a one-time donation through PayPal. Links are in the video description. And now again, really, goodbye for now and Fröhliche Weihnachten.